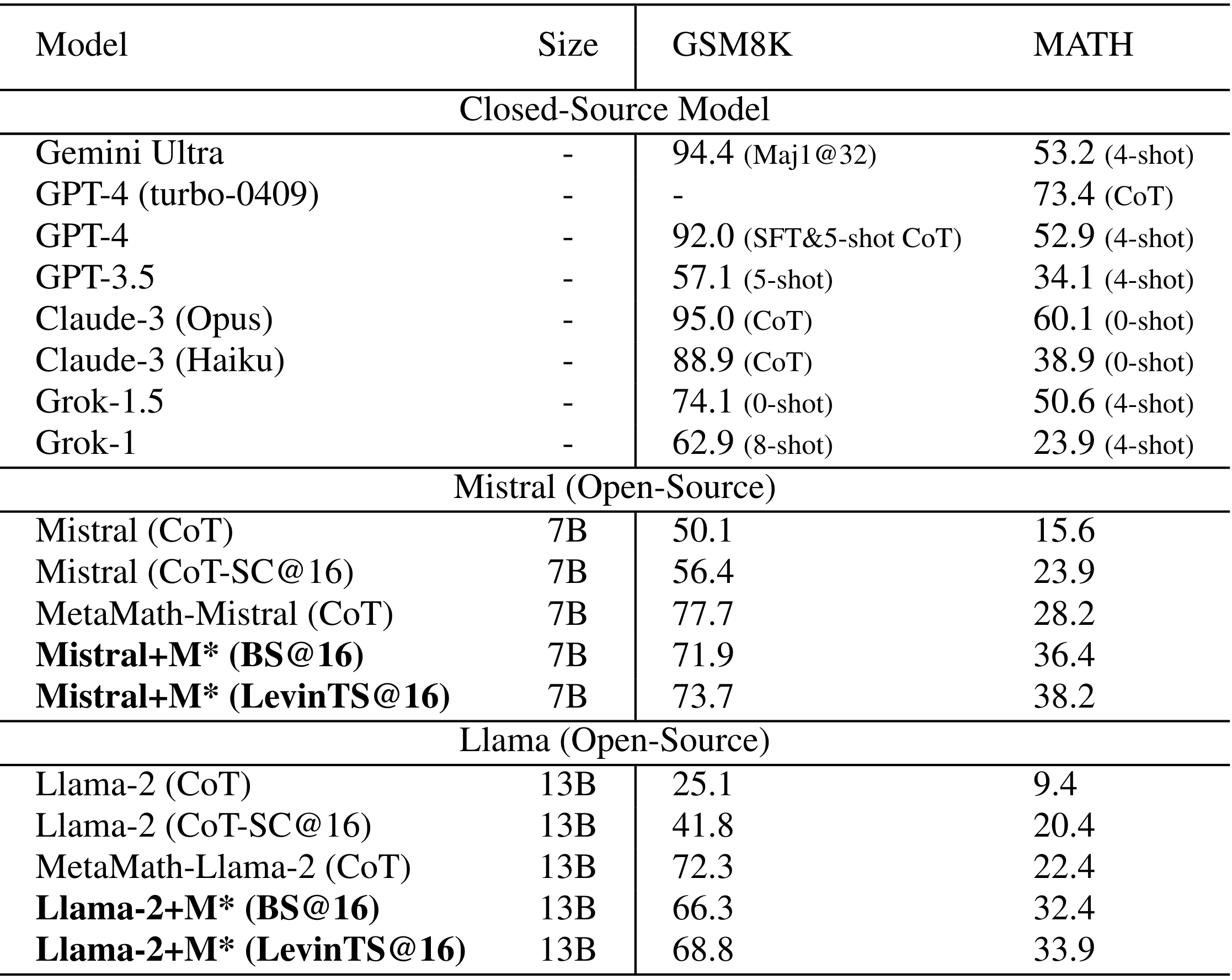
Although Large Language Models (LLMs) achieve remarkable performance across various tasks, they often struggle with complex reasoning tasks, such as answering mathematical questions. Recent efforts to address this issue have primarily focused on leveraging mathematical datasets through supervised fine-tuning or self-improvement techniques. However, these methods often depend on high-quality datasets that are difficult to prepare, or they require substantial computational resources for fine-tuning. Inspired by findings that LLMs know how to produce the right answer but struggle to select the correct reasoning path, we propose a purely inference-based searching method---MindStar (M*). This method formulates reasoning tasks as searching problems and proposes two search ideas to identify the optimal reasoning paths. We evaluate the M* framework on both the GSM8K and MATH datasets, comparing its performance with existing open and closed-source LLMs. Our results demonstrate that M* significantly enhances the reasoning abilities of open-source models, such as Llama-2-13B and Mistral-7B, and achieves comparable performance to GPT-3.5 and Grok-1, but with substantially reduced model size and computational costs.
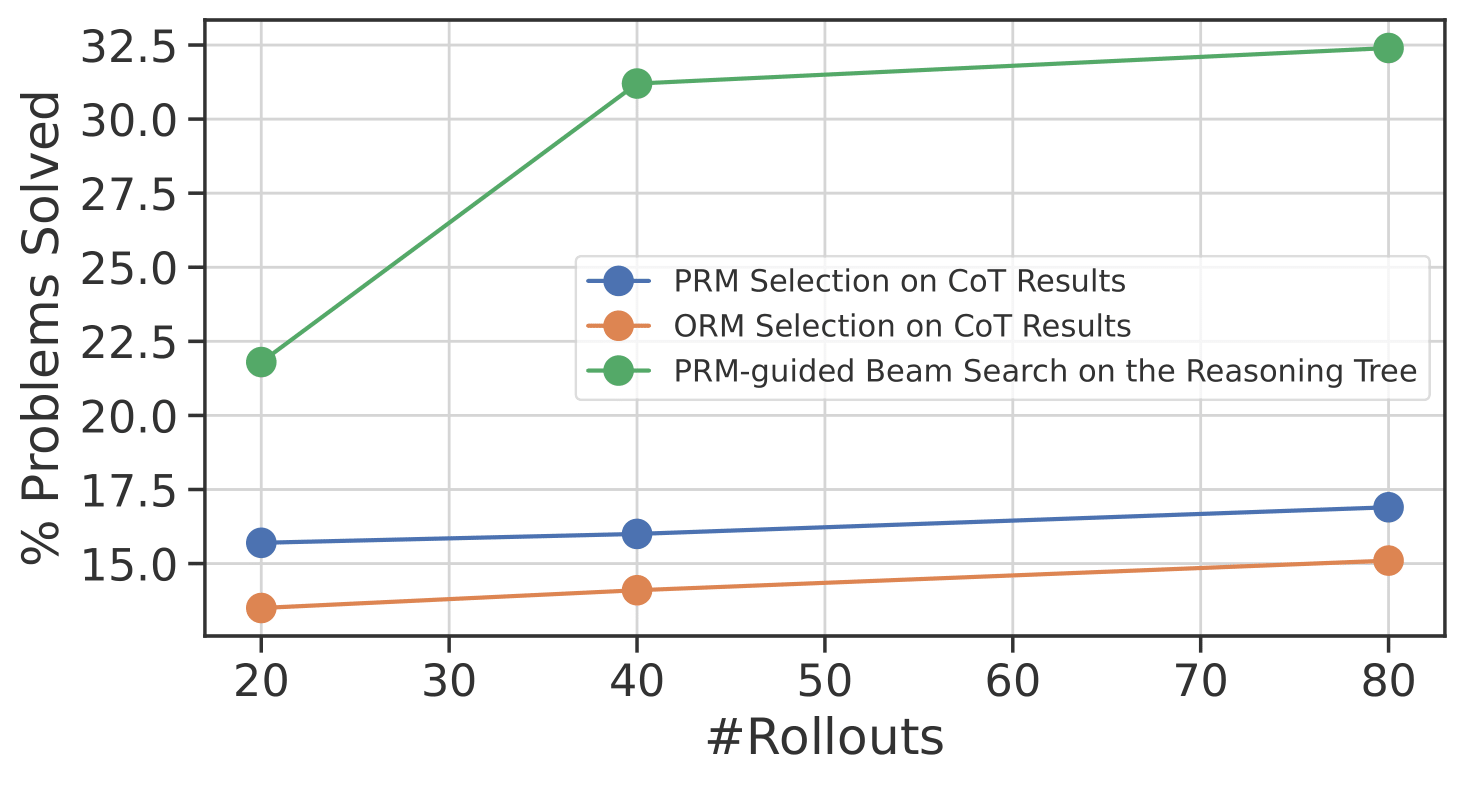
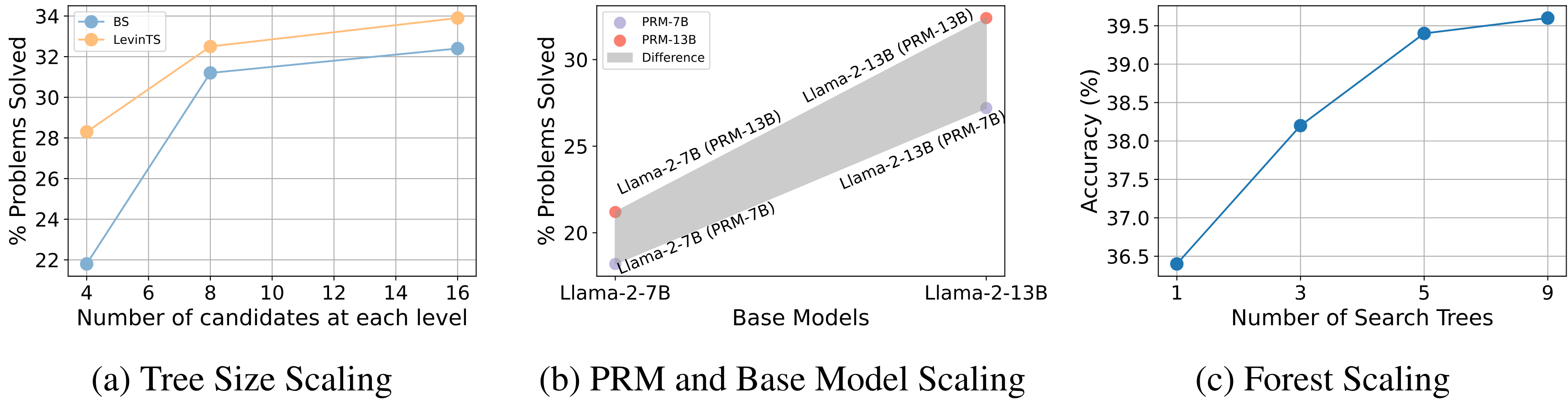
To explore this, we conduct an experiment utilizing different reward models to assist LLM for output selection. Here, we leverage the Outcome-supervised Reward Model (ORM), which scores the entirety of reasoning solutions, and the Process-supervised Reward Model (PRM), which scores each individual reasoning step, for the selection of reasoning solutions. Initially, we apply both the ORM and the PRM to select the final answer from multiple sampled chain-of-thoughts (CoT) solutions. The figure below shows that PRM selects better reasoning answers than ORM. Additionally, we employ the PRM to assist the LLM in a tree-of-thought context; Rather than generating the complete solution, the LLM produces multiple intermediate steps. The PRM then scores these steps and selects the best, facilitating the LLM in proceeding generation from a promising step. Our results demonstrate that step-level selection outperforms the two CoT selection baselines significantly.
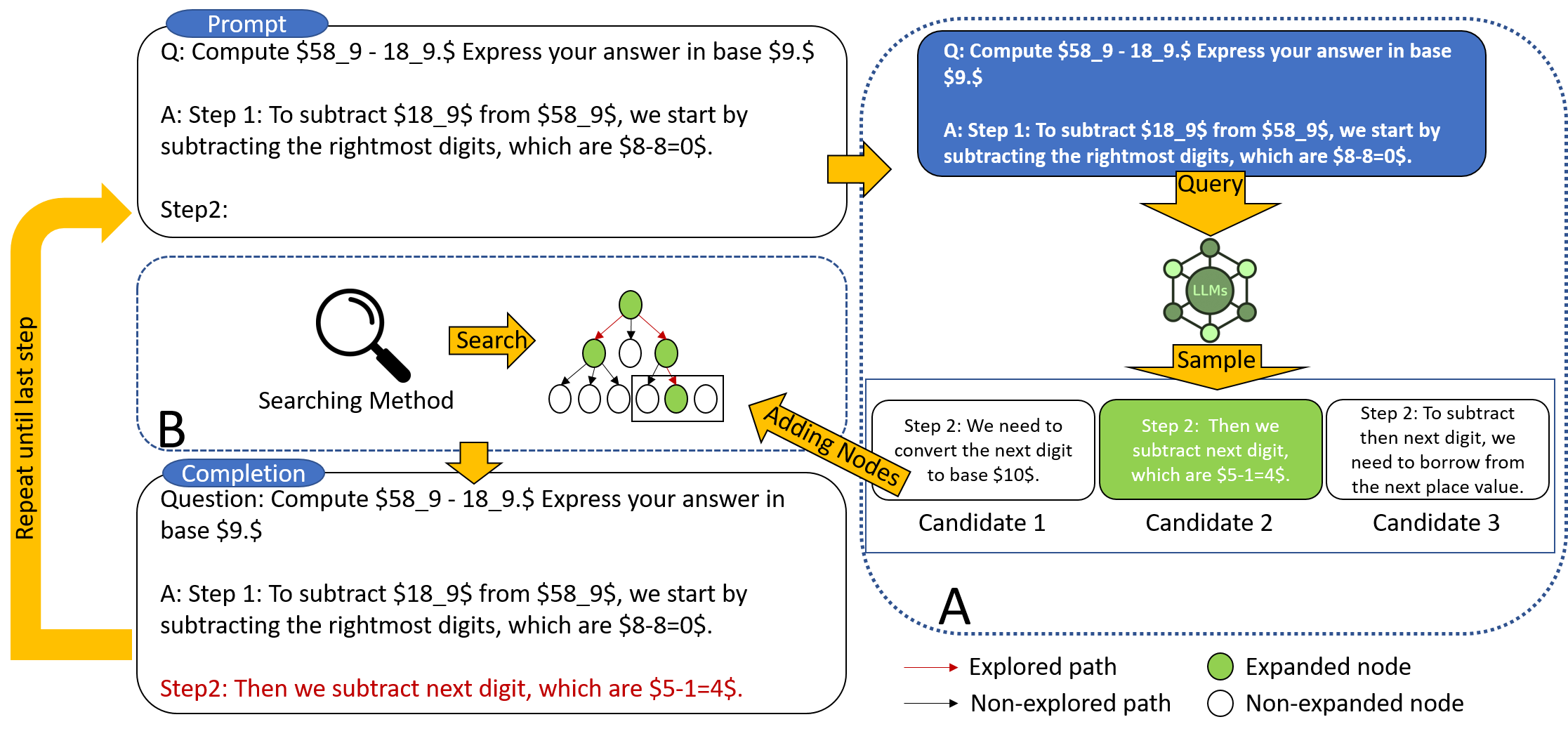
Given that we select a reasoning node \(n_d\) to expand, we design a prompt template Example 3.1 in order to collect next steps from LLMs. As shown in the example, the LLM takes the original question as \{question\} and the current reasoning path as \{answer\} in the prompt. Note that in the first iteration of the algorithm, the selected node is the root containing the question only, and therefore the \{answer\} is empty. For the reasoning path \(n_d\), the LLM generates \(N\) multiple intermediate steps \(e^1_{d}, e^2_{d}, \dots, e^N_{d}\) for the given prompt and we append them as the children node of the current node. In the next step of the algorithm, the new child nodes will be assessed, and a new node will be selected for further expansion. We also acknowledge that one alternative for generating the steps is fine-tuning the LLM using step tokens. However, it could potentially degrade the LLM's reasoning ability and, more importantly, is not aligned with the focus of this paper which, is enhancing the LLM without any weight modification.

Following the reasoning node expansion, we use the pre-trained PRM \(\mathcal{P}\) to reflect each newly generated step. The PRM takes the path \(n_d\) and the steps \(e_d\) as inputs and returns the corresponding reward value. After the evaluation, we require a tree search algorithm to select the next node for expansion. Note that our framework is agnostic to the search algorithm, and in this work, we instantiate it with two tree search methods, namely beam search and Levin tree search. Additionally, we introduce an ensemble method of M* search as an extension - Forest Search.

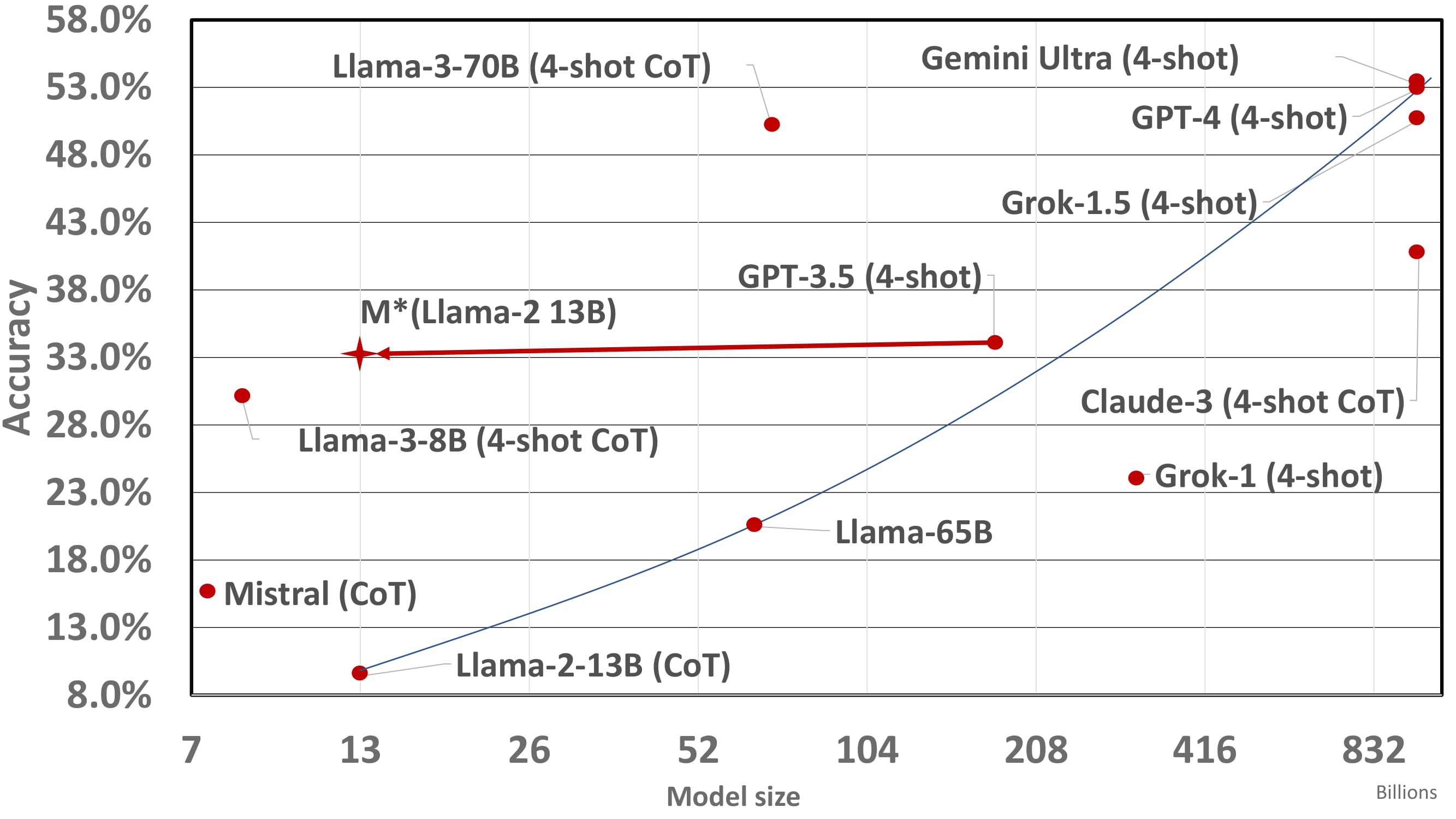
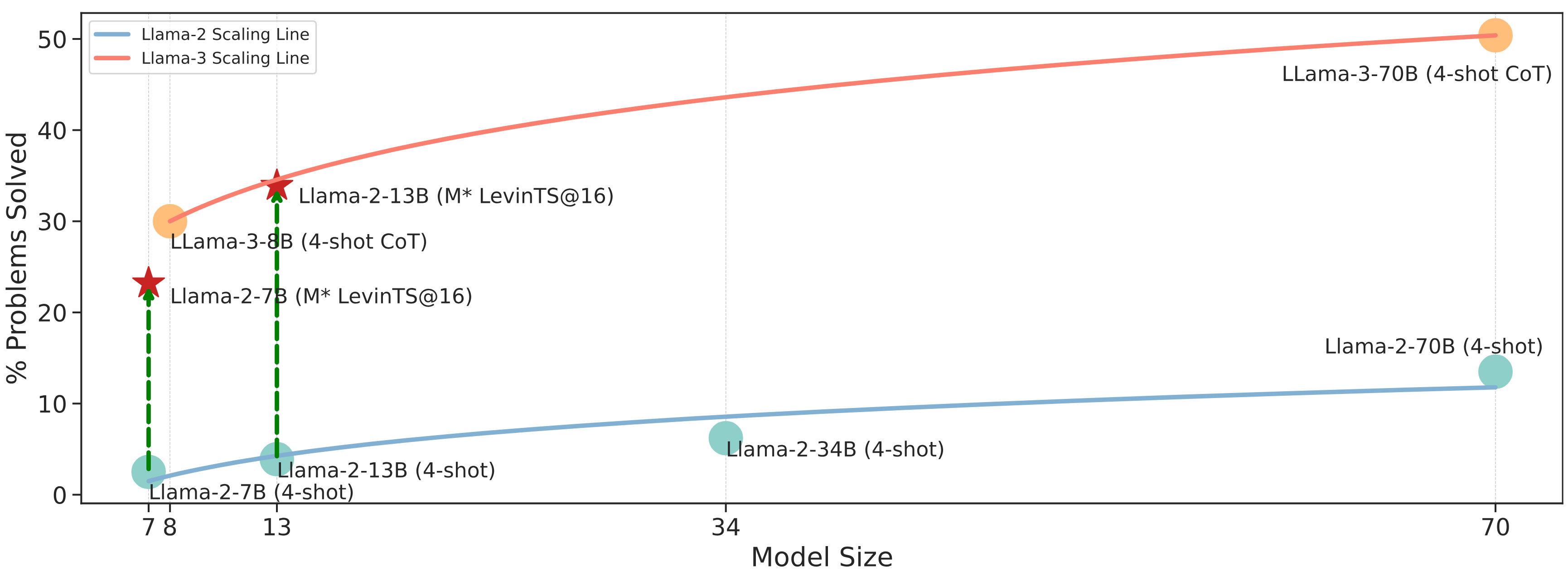
In our investigation of scaling laws within the Llama family of models, notably Llama-2 and Llama-3, we applied the M* method to observe its impact on performance improvement relative to model size. As illustrated in below, the application of M* substantially enhances the performance of the Llama-2 model, aligning its scaling trajectory closer to that of the Llama-3 model. This improvement in scaling efficiency through the M* method is significant because it suggests that the reasoning capabilities of LLMs can be enhanced without necessarily increasing the volume of high-quality training data. Instead, the focus shifts toward selecting right responses, thereby conserving resources while still achieving competitive performance metrics.
@article{kang2024mindstar,
title={MindStar: Enhancing Math Reasoning in Pre-trained LLMs at Inference Time},
author={Kang, Jikun and Li, Xin Zhe and Chen, Xi and Kazemi, Amirreza and Sun, Qianyi and Chen, Boxing and Li, Dong and He, Xu and He, Quan and Wen, Feng and Hao, Jianye and Yao, Jun},
journal={arXiv preprint arXiv:2405.16265},
year={2024}
}